Question

What is the discontinuity and zero of the function f(x) = the quantity of 3 x squared plus x minus 4, all over x minus 1? A. Discontinuity at (-1, 1), zero at (four thirds, 0) B. Discontinuity at (-1, 1), zero at (negative four thirds , 0) C. Discontinuity at (1, 7), zero at (four thirds , 0) D. Discontinuity at (1, 7), zero at (negtive four thirds, 0)

Answer 1

The correct option is D. Discontinuity at (1, 7), zero at (negative four thirds, 0)

Explanation:

`\text{The function is given to be : }f(x)=(3x^2+x-4)/(x-1)\\\\\implies f(x)=((3x+4)(x-1))/((x-1))`

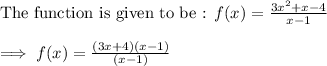
To find the point of discontinuity :

Put the denominator equal to 0

⇒ x - 1 = 0

⇒ x = 1

Also, if the factor (x - 1) gets cancel, then it becomes a hole rather than a asymptote , ⇒ y = 3x + 4 at x = 1

⇒ y = 7

So, Point of discontinuity : (1, 7)

And the zero is : after cancelling the factor (x - 1) put the remaining factor = 0

⇒ 3x + 4 = 0

⇒ 3x = -4

⇒ x = negative four thirds ( zero of the function)

Therefore, The correct option is D. Discontinuity at (1, 7), zero at (negative four thirds, 0)

Answer 2

The discontinuity is at (1, 7) and the zero is at (negative four thirds, 0) for the function f(x) = the quantity of 3 x squared plus x minus 4, all over x minus 1.

The correct answer between all the choices given is the last choice or letter D. I am hoping that this answer has satisfied your query and it will be able to help you in your endeavor, and if you would like, feel free to ask another question.