Question

Which statement about the following equation is true?

2x^2 – 9x + 2 = –1

A.) The discriminant is less than 0, so there are two real roots.
B.) The discriminant is less than 0, so there are two complex roots.
C.) The discriminant is greater than 0, so there are two real roots.
D.) The discriminant is greater than 0, so there are two complex roots.

Answer 1

The answer is C). The discriminant is greater than 0, so there are two real roots.

Explanation:

Plz give credit to the other guys answer bc it is well thought out and deserves 5 stars!!!

Answer 2

Option C is correct that is the discriminant is greater than 0, so there are two real roots.

Explanation:

We have been given the quadratic equation:

`2x^2-9x+2=-1`

We will rearrange the like terms and so the equation will become:

`2x^2-9x+2+1=0`

`\Rightarrow 2x^2-9x+3=0`

We will solve the above quadratic equation by discriminant rule

Where,
`D=b^2-4ac`

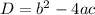
We will compare the equation with general quadratic equation

Here, a=2,b= -9 and c=3 on substituting the values we get:

`D=(-9)^2-4(2)(3)=57\geq0`

Therefore, Option C is correct that is the discriminant is greater than 0, so there are two real roots.