Question

The function f(t) = 4t2 - 8t + 7 shows the height from the ground f(t), in meters, of a roller coaster car at different times t. Write f(t) in the vertex form a(x - h)2 + k, where a, h, and k are integers, and interpret the vertex of f(t).

A.) f(t) = 4(t - 1)2 + 3; the minimum height of the roller coaster is 3 meters from the ground
B.) f(t) = 4(t - 1)2 + 3; the minimum height of the roller coaster is 1 meter from the ground
C.) f(t) = 4(t - 1)2 + 2; the minimum height of the roller coaster is 2 meters from the ground
D.) f(t) = 4(t - 1)2 + 2; the minimum height of the roller coaster is 1 meter from the ground

Answer 1

Option A-
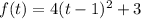`f(t)=4(t-1)^2+3` ; the minimum height of the roller coaster is 3 meters from the ground.

Explanation:

Given : The function
`f(t) = 4t^2-8t+7` shows the height from the ground f(t), in meters, of a roller coaster car at different times t.

To find : Write f(t) in the vertex form
`a(x - h)^2 + k`, where a, h, and k are integers, and interpret the vertex of f(t).

Solution :

We have given the function
`f(t) = 4t^2-8t+7`

As the leading coefficient is 4 which is positive, so the parabola will open upward and at the vertex the value of the function will be minimum.

Now, we convert it into vertex form,

`f(t)=4t^2-8t+7`

`f(t)=4(t^2-2t)+7`

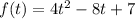
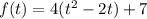
Making completing square,

`f(t)=4(t^2-2t+1^2-1^2)+7`

`f(t)=4(t^2-2t+1^2)-4+7`

`f(t)=4(t-1)^2+3`

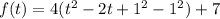
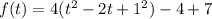
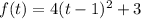
So the vertex form will be,
`f(t)=4(t-1)^2+3`

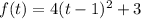
Where Vertex are (h,k)=(1,3) and a=4

At vertex the value of the function f(t) is 3.

So, the minimum height of the roller coaster is 3 meters from the ground.

Therefore, Option A is correct.

Answer 2

A.
`f(t)=4(t-1)^2+3`; the minimum height of the roller coaster is 3 meters from the ground.

Explanation:

The given function is,

`f(t) = 4t^2 - 8t + 7`

As the leading coefficient is 4 which is positive, so the parabola will open upward and at the vertex the value of the function will be minimum.

`f(t)=4t^2-8t+7`

`=4(t^2-2t)+7`

`=4(t^2-2\cdot t\cdot 1+1^2-1^2)+7`

`=4(t^2-2\cdot t\cdot 1+1^2-1)+7`

`=4(t^2-2\cdot t\cdot 1+1^2)-4+7`

`=4(t^2-2\cdot t\cdot 1+1^2)+3`

`=4(t-1)^2+3`

So the vertex form will be,

`f(t)=4(t-1)^2+3`

Hence the vertex will be at
`(1,3)`

At vertex the value of the function ot f(t) is 3, so the minimum height of the roller coaster is 3 meters from the ground.