Answer:
Option C is correct.
The equation of line is , f(x)=2x+5
Explanation:
Point slope intercept form: For any two points
 and
and
 then,
then,
the general form of the equation of line is given by;
 ; where m is the slope given by:
; where m is the slope given by:
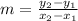
Consider the given points;
(1, 7) and (5 , 15)
First calculate the slope (m);
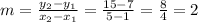
Therefore, slope of the line, m=2
Then, the equation of line is:

Substitute the value of m=2 and (1, 7) above we get;
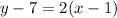
or
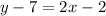
Add 7 to both sides of an equation we get;
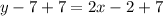
Simplify:
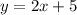
using function notation i.e, y =f(x)
then, we have f(x) = 2x+5
therefore, the equation of line that passes through the point (1, 7) and (5, 15) is ; f(x)=2x+5