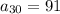Question

What is the 30th term of the arithmetic series 4, 7, 10, … ?

Answer 1

`a_1=4;\ a_2=7;\ a_3=10\\\\d=a_2-a_1\to d=7-4=3\\\\a_n=a_1+(n-1)d\to a_n=4+(n-1)\cdot3=4+3n-3=3n+1\\\\\boxed{a_n=3n+1}\\\\a_(30)=3\cdot30+1=90+1=91\\\\Answer:\boxed{a_(30)=91}`

Answer 2

`a_(30)=91`

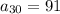
Explanation:

Given : an arithmetic sequence 4, 7, 10,....

We have to find the 30th term of the given arithmetic series.

Consider the given arithmetic sequence 4, 7, 10,....

Here,

`a_1=4\\\\ a_2=7\\\\ a_3= 10`

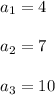
We first find the common difference (d),

`a_2-a_1=7-4=3`

`a_3-a_2=10-7=3`

Since, the difference between the terms are same so the common difference is 3.

The formula for the general term in an arithmetic series is given by

`a_n= a+(n-1)d`

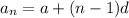
Where , n is the number i=of the term,

a is first term

d is common difference,

Since, we have to find the 30 th term,

So put n = 30 , d = 3 , a= 4

We have,

`a_(30)=4+(30-1)3`

Simplify, we have,

`a_(30)=4+29* 3`

`a_(30)=4+29* 3`

Thus,
`a_(30)=91`