Answer:
The correct option is B
Explanation:
The formula for confidence interval for the mean is
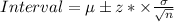
Where, μ is population mean, σ is standard deviation, n is sample size and z* is z-score at given confidence interval.
From the z-table the value of z-score at 98% confidence interval is 2.33.
From the given information it is clear that
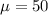

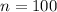
The 98% confidence interval for the mean hours devoted to social networking in January is
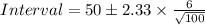

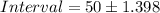
![Interval=[50-1.398,50+1.398]](https://img.qammunity.org/2017/formulas/mathematics/middle-school/ev99jbxgzi3nkajwkvjyoxjja94p5zznjl.png)
![Interval=[48.602,51.398]](https://img.qammunity.org/2017/formulas/mathematics/middle-school/o14d6eyelcljtuo9xespq32r6yc9faig3u.png)
![Interval=[48.60,51.40]](https://img.qammunity.org/2017/formulas/mathematics/middle-school/dz9aus13nzukpxkqtqspg60ehztxhnw3zb.png)
Therefore the 98% confidence interval ranges from 48.60 to 51.40 hours. Option B is correct.