Question

About how accurately must the interior diameter of a 10-m high cylindrical storage tank be measured to calculate the tank's volume within 1% of its true value?. . About how accurately must the tank's exterior diamter be measured to calculate the amount of paint it will take to paint the side of the tank to within 5% of the true amount?

Answer 1

Answer: The correct answers are half percentage and 2.5 percentage.

Step-by-step explanation:

The volume of the cylinder is as follows;

`V=\pi r^(2)h` ....... (1)

Here, r is the radius and h is the height.

On differentiating on the both side.

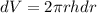`dV=2\pi rhdr` ........ (2)

Divide (2) by (1).

`(dV)/(V)=(2\pi rhdr)/(\pi r^(2)h)`

`(dV)/(V)=(2dr)/(dr)`

`(dr)/(r)=(1)/(2)(dV)/(V)`

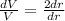
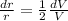
Put
`(dV)/(V)=1%`

`(dr)/(r)=(1)/(2)1%`

`(dr)/(r)=.005`

`(dr)/(r)=0.5%`

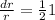
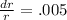
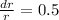
To get the volume within 1% measure the radius (or the diameter) must be within half percentage of the true radius (or the diameter).

`(dr)/(r)=(1)/(2)(dV)/(V)`

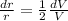
Put
`(dV)/(V)=5%`

`(dr)/(r)=(1)/(2)5%`

`(dr)/(r)=0.025`

`(dr)/(r)=2.5%`

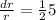
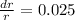
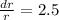
To get the volume within 2.5% measure the radius (or the diameter) must be within half percentage of the true radius (or the diameter).

Answer 2

V = (pi) * R^2 * H

dV = 2 * (pi) * R * H * (dR)

dV/V = 2 * (pi) * R * H * (dR) / (pi) * R^2 * H = 2 * (dR) / R

2 * (dR) / R = dV/V

dR/R = 1/2 * dV/V

dV/V * 100 is the percentage error in volume calculation = 1%

dV/V = 1/100 = .01

Therefore, dR/R = 1/2 * dV/V = 1/2 * .01 = .005 or 0.5%

The percentage error in measuring the radius (or the diameter) must be within 0.5% of the true radius (or the diameter) in order to calculate the tank's volume within 1% of its true value.