Question

The product of two consecutive integers is 420. An equation is written in standard form to solve for the smaller integer by factoring.

What is the constant of the quadratic expression in this equation?

x2 + x + ___ = 0

Answer 1

x(x + 1) = 420
x^2 + x = 420
x^2 + x + (- 420) = 0 or x^2 + x - 420 = 0

Answer 2

• The product of two consecutive integers is 420:

20*21 = 420 and (-21)*(-20) = 420

• What is the constant of the quadratic expression in this equation?

Any constant less or equal than 0.25

Explanation:

The product of two consecutive integers is 420 can be expressed mathematically as follows:

x*(x+1) = 420

After applying distributive property and subtracting 420 at both sides, we get:

x^2 + x - 420 = 0

In order to factorise, we use the quadratic equation as follows:

`x = (-b \pm √(b^2-4(a)(c)))/(2(a))`

`x = (-1 \pm √(1^2-4(1)(-420)))/(2(1))`

`x = (-1 \pm √(1681))/(2)`

`x = (-1 \pm 41)/(2)`

`x_1 = (-1 + 41)/(2)`

`x_1 = 20`

`x_2 = (-1 - 41)/(2)`

`x_2 = -21`

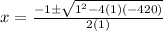
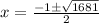
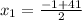
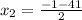
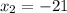
Then, 20*21 = 420 and (-21)*(-20) = 420

A quadratic equation with the standard form has a solution to the equation: a*x^2 + b*x + c = 0 if its discriminant is greater or equal than zero. Mathematically:

b^2-4(a)(c) >= 0

Here a = 1 and b = 1; then,

1^2-4(1)(c) >= 0

-4(c) >= -1

c <= -1/-4

c <= 0.25