Question

. . A new car depreciates at a rate of 15% per year. What is the expected value of a $25,000 car after 5 years (rounded to nearest whole dollar)? . . . . . . . . . . . . A). $20750 . . B). $11093 . . C). $9429 . . D). $6250 . .

Answer 1

You might have lacking given information so you can re-check the given.
You are lacking the value of L (life of the car in years).

There are several types of depreciation formulas. The straight-line method, sinking fund method, declining balance and double-declining balance. For the other methods you can search it up.

I used the sinking fund method for this case:

d = \frac{(25000 - 0)*0.15}{(1+0.15)^{L} -1

where d is the annual cost of depreciation
Co is the original cost,

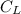`C_(L)` is the value at the end of the life of object or salvage value
L is useful life of the property
and i is the interest rate.

The salvage value can be assumed as zero in this case, therefore,

`d = ((25000 - 0)*0.15)/((1+0.15)^(L) -1)`

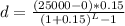
In solving for the expected depreciation one can use this formula:

`D_n = d*((1 + i)^(n)-1 )/(i)`
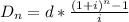
where n is the number of years of the expected depreciation
D_n is the depreciation up to the number of years (n)

Answer 2

The answer to the question above is letter B. The new car depreciates at the rate of 15% per year. The expected value of the car after 5 years is $11,093. to explain the calculation of the answer :

year amount % interest total
1 25000 0.15 3750 21250
2 21250 0.15 3187.5 18062.5
3 18062.5 0.15 2709.375 15353.13
4 15353.13 0.15 2302.969 13050.16
5 13050.16 0.15 1957.523 11092.63