Question

How many different ways could a baking contest be judged if 15 pies are entered and 4 ribbons are awarded?

Answer 1

1365

Explanation:

We are given that 15 pies are entered in the contest.

Out of 15 , 4 are awarded with ribbons.

Now we are supposed to find How many different ways could a baking contest be judged.

Since the order of pie doesn't matter over here.

So, we will use combination.

`^nC_r=(n!)/(r!(n-r)!)`

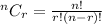
Substitute n = 15

r = 4

So,
`^(15)C_4=(15!)/(4!(15-4)!)`

`^(15)C_4=(15!)/(4!(11)!)`

`^(15)C_4=(15 * 14* 13 * 12 * 11!)/(4!(11)!)`

`^(15)C_4=(15* 14* 13 * 12)/(4* 3 * 2* 1)`

`^(15)C_4=1365`

Hence there are 1365 ways in which a baking contest could be judged.

Answer 2

This is a question of combination since it does not take into account the order of the pies. The answer would be 1365. There are 1365 ways a baking contest ways can be judged if 4 ribbons are awarded with 15 pie entries.

In case you need the order, then the permutation answer would be 32760.