Question

An automobile engineer is redesigning a conical chamber that was originally specified to be 12 inches long with a circular base of diameter 5.7 inches. In the new design, the chamber is scaled by a factor of 1.5. The volume of the original chamber is a.)102.02 b.)248.04 c.)306.06 d.)412.08 cubic inches. This is a.)242.47 b.)344.49 c.)432.16 d.)448.21 cubic inches less than the volume of the new chamber.

Answer 1

a and a

Explanation:

Answer 2

The answers are:
a.)102.02
a.)242.47

The volume of the cone can be expressed as:

`V = (1)/(3) \pi r^(2) h`
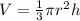
where:
V - the volume of the cone,
r - the radius of the cone,
h - the height of the cone.

It is given:
h = 12 in
R = 2r = 5.7 in ⇒ r = 5.7 in ÷ 2 = 2.85 in
π = 3.14

Therefore, the volume of the original conical chamber (V₁)

`V = (1)/(3) *3.14*(2.85) ^(2) *12 = 3.14*8.1225*4 = 102.02 in^(3)`


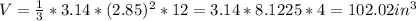
Further, the new chamber is scaled by a factor of 1.5. That means that radius and height of the original chamber are increased 1.5 times:
r₁ = r · 1.5 = 2.85 in · 1.5 = 4.275 in
h₁ = h · 1.5 = 12 in · 1.5 = 18 in

The volume of the new chamber is:

`V_1= (1)/(3) *3.14*(4.275) ^(2) *18 = 3.14*18.28*6=344.49 in ^(3)`

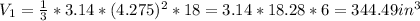
The difference between two chambers is:
V₁ - V = 344.49 - 102.02 = 242.47