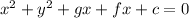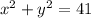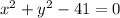Question

What is the general form of the equation for the given circle centered at O(0, 0)? The center is (0,0) the point on the circle is (4,5)

Answer 1

Hello,

Radius= √((4-0)²+(5-0)²)=√41
Equation of the circle : x²+y²=41

Answer 2

`x^2+y^2-41=0`

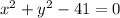
Explanation:

Center of the circle is (0,0)

the point on the circle is (4,5)

Center radius form of the circle is

`(x-h)^2 +(y-k)^2= r^2`

where (h,k) is the center and 'r' is the radius of the circle

WE know center is (0,0) . Lets find out the radius using the given point

`(x-0)^2 +(y-0)^2= r^2`

`x^2+y^2= r^2`

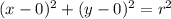
Plug in the given point (4,5)

`4^2+5^2= r^2`

`16+25= r^2`

`41=r^2`

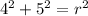
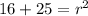
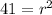
Equation becomes

`x^2+y^2=41`

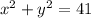
General form of equation is

`x^2+y^2+gx+fx+c=0`

`x^2+y^2=41`

`x^2+y^2-41=0`