Question

In a video game, two golfers tee off at hole 6, which has the coordinates (–32, –27). Golfer A’s ball lands at (–43, –18). Golfer B’s ball lands at (–44, –16). Which golfer hit the longer shot?

Answer 1

Using Pythagoras' theorem, you can work out the distance the balls travelled.
Golfer A: -43 - -32 = -43 + 32 = -11
-27 - -16 = -27 + 16 = -11
a² + b² = c²
(-11)² + (-11)² = √242 = 15.556

Golfer B: -44 - -32 = -44 + 32 = -12
-27 - -16 = -27 + 16 = -11
a² + b² = c²
(-11)² + (-12)² = √265 = 16.278

∴ B hit the longest shot.

Answer 2

Golfer B's hit the longer shot.

Explanation:

In a video game, two golfers tee off at hole 6

Position of hole at (-32,-27)

Golfer A's ball lands at (-43,-18)

Golfer B's balls lands at (-44,-16)

Distance formula:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

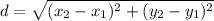
Distance of shot of Golfer A's
`=√((-32+43)^2+(-27+18)^2)=√(11^2+9^2)\approx 14.21`

Distance of shot of Golfer B's
`=√((-32+44)^2+(-27+16)^2)=√(12^2+11^2)\approx 16.28`

16.28 > 14.21

Golfer B's shot > Golfer A's shot

Hence, Golfer B's hit the longer shot.