Question

Dahlia is trying to decide which bank she should use for a loan she wants to take out. In either case, the principal of the loan will be $19,450, and Dahlia will make monthly payments. Bank P offers a nine-year loan with an interest rate of 5.8%, compounded monthly, and assesses a service charge of $925.00. Bank Q offers a ten-year loan with an interest rate of 5.5%, compounded monthly, and assesses a service charge of $690.85. Which loan will have the greater total finance charge, and how much greater will it be? Round all dollar values to the nearest cent.

a.
Loan Q’s finance charge will be $83.73 greater than Loan P’s.
b.
Loan Q’s finance charge will be $317.88 greater than Loan P’s.
c.
Loan P’s finance charge will be $20.51 greater than Loan Q’s.
d.
Loan P’s finance charge will be $234.15 greater than Loan Q’s.

Answer 1

a. Loan Q’s finance charge will be $83.73 greater than Loan P’s.

Explanation:

Answer 2

To solve this, we are going to use the loan payment formula:
`P= ( (r)/(n)(PV))/(1-(1+ (r)/(n))^(-nt) )`

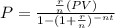
where

`P` is the payment

`PV` is the present debt

`r` is the interest rate in decimal form

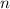`n` is the number of payments per year

`t` is the time in years

For Bank P

We know from our problem that the the principal of the loan will be $19,450, so
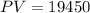`PV=19450`. We also know that Bank P offers a nine-year loan with an interest rate of 5.8%, compounded monthly , so
`t=9` and
`r=(5.8)/(100) =0.058`. Since Dahlia will make monthly payments, and a there are 12 months in a year,
`n=12`. Lets replace the values in our formula:

`P= ( (r)/(n)(PV))/(1-(1+ (r)/(n))^(-nt) )`

`P= ( (0.058)/(12)(19450))/(1-(1+ (0.058)/(12))^(-(12)(9)) )`

`P=231.59`

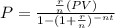
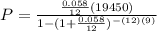
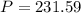
Now we know that the monthly payment of Dahlia is $231.59. Since we know that she is going to make 12 monthly payments for 9 years, we can calculate the future value of the loan multiplying the amount of the monthly payments ($231.59) by the number of monthly payments (12) by the number of years (9):

`FV=(231.59)(12)(9)`

`FV=25011.72`

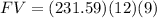
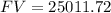
Now we know that she is is going to pay $25,011.72 for her loan. Finally, to calculate the total finance charge, we are going to subtract the original loan ( $19,450) from the future value of the loan ($25,011.72), and then, we are going to add the service charge ($925.00):

`FinanceCharge=(25011.72-19450)+925`

`FinanceCharge=6486.72`

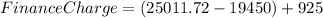
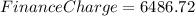
The total finance charge of bank P is $6,486.72

For Bank Q

We are going to repeat the same procedure as before.

`P=19450`,
`r=(5.5)/(100) =0.055`,
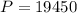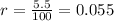`n=12`, and
`t=12`. Lets replace the values in our formula:

`P= ( (0.055)/(12)(19450))/(1-(1+ (0.055)/(12))^(-(12)(10)) )`

`P=211.08`

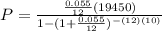
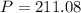
Now that we have our monthly payment, we can calculate the future value of the loan multiplying the amount of the monthly payments ($211.08) by the number of monthly payments (12) by the number of years (10):

`FV=(211.08)(12)(10)`

`FV=25329.6`

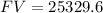
Just like before, to calculate the total finance charge, we are going to subtract the original loan ( $19,450) from the future value of the loan ($25,329.6), and then we are going to add the service charge ($690.85):

`FinanceCharge=(25329.6-19450)+690.85`

`FinanceCharge=6570.45`

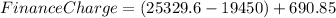
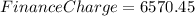
The total finance charge of bank Q is $6570.45

Notice that the finance charge of ban Q is greater than the finance charge of bank P, so we are going to subtract the finance charge of bank Q from the finance charge of bank P:

`6570.45-6486.72=83.73`

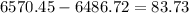
We can conclude that Loan Q’s finance charge will be $83.73 greater than Loan P’s. Therefore, the correct answer is a.