The leaning tower of pisa is cylindrical and as such the volume can be approximated using the same formula as a regular cylinder.
Volume of a cylinder (V) =

Assume
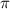
=
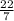
V = 9891
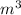
h = 56 m
Let: Radius= r
Diameter= D
Then D= 2r
By substituting the known values into the equation and transposing one can formulate an equation to solve for D.
V
=

: . 9891
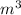 =
=
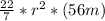
Making r the subject of this equation:
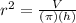
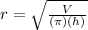
Since the Diameter is 2r then multiply both sides of the equation by 2
: .
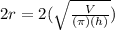
thus D =
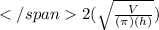
Part B:
Since the formula for Diameter has be formulated, substitute the values of the variables and solve for D
D =
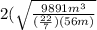
: . D =

= 2 * 7.497m
= 14.993 m
Part C:
Therefore it can be concluded that the Diameter of the base of the Leaning Tower of Pisa is approximately 14.99 meters.