Question

The function t(x) = x + 6 determines how many cans of soup a food truck needs to stock, where x is the number of shifts the crew is going to work in the truck. The crew uses c(t(x)) to find the amount of money to spend on soup. The function c(x) = 2x + 4. Solve for how much money must be spent when the crew is going to work 4 shifts.

(A. 24; B. 28; C. 30; D. 34)

Answer 1

First, you have to solve t(x) when x=4, because the crew is working 4 scripts. Which is t(x)=4+6
t(x)=10
Then, you plug in t(x) to c(x).
c(x)=2(10)+4
c(x)=24

Answer 2

Option A is correct.

The amount of money must be spent when the crew is going to work 4 shifts is, 24

Explanation:

Given the function:
`t(x) = x+6` .....[1] ; where x represents the number of shifts the crew is going to work in the truck.

Also, the crew uses c(t(x)) which represents the amount of money to spend on soup.

The function is given as:

c(x) = 2x + 4 .....[2]

To find c(t(x)) i.e, the money must be spent when the crew is going to work 4 shifts.

⇒ x = 4

First substitute the value of x in [1] to find t(x);

`t(4) = 4+6 = 10`

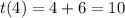
Then;

For x=4 ,

c(t(4)) = 2(t(4)) +4 [Using equation [2]]

Substitute the value of t(4) = 10 we have;

c(t(4)) = 2(10) +4 = 20 + 4 = 24

Therefore, the amount must be spent when the crew is going to work 4 shifts is, 24