Question

According to the Fundamental Theorem of Algebra, how many roots exist for the polynomial function?

(9x + 7)(4x + 1)(3x + 4) = 0

Answer 1

3

To obtain result 0 u need result 0 in one of that bracket.

For first one it's -7/9
Second -1/4
3'rd -4/3

Answer 2

Three roots exist of given polynomial.

Explanation:

Given:
`(9x+7)(4x+1)(3x+4)=0`

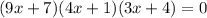
Fundamental theorem of algebra: It states that each factor of polynomial with complex coefficient must be atleast one complex root.

If polynomial with real coefficients then their complex root with zero imaginary part.

In the given polynomial,
`(9x+7)(4x+1)(3x+4)=0`

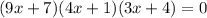
Each term as factor factor. Here we have total three factor. If we set each factor to 0 and solve for x. We will get root for each value of x.

So, Here should be three roots possible.

`9x+7=0\Rightarrow x=-(7)/(9)`

`4x+1=0\Rightarrow x=-(1)/(4)`

`3x+4=0\Rightarrow x=-(4)/(3)`

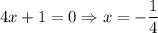
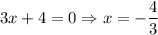
All roots are real.

Hence, Three roots exist of given polynomial.