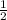Question

A sequence of numbers begins with 12 and progresses geometrically. Each number is the previous number divided by 2.

Which value can be used as the common ratio in an explicit formula that represents the sequence?


2
6
12

Answer 1

Common ratio =
`(1)/(2)`

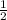
Explanation:

A sequence that progresses geometrically has the first term as 12.

Each number is the previous number divided by 2.

so the sequence will be 12, 6, 3, 1.5...........

Explicit formula of a geometric sequence is given by

`T_(n)=a(r)^(n-1)`

Where
`T_(n)` = nth term of the sequence

a = first term

r = common ratio

and n = number of term

In this sequence common ratio =
`\frac{\text{Successive term}}{\text{previous term}}`

=
`(6)/(12)`

=
`(1)/(2)`

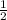
Therefore, common ratio will be
`(1)/(2)`

Answer 2

The common ratio is the current number divided by the previous. So the ratio is 1/2

The sequence is 12, 6, 3, 3/2, 3/4 ...

You can obtain any number multiplying the previous number times 1/2.

6 = 12 *(1/2)

3 = 6*(1/2)

3/2 = 3*(1/2)