Question

f(5)=12 for a geometric sequence that is defined recursively by the formula f(n)=0.3*f(n-1), where n is an integer and n>0. Find f(7). Round your answer to the nearest hundredth.

Answer 1

f(7) = 1.08

Explanation:

Given that:

f(5) = 12

A geometric sequence that is defined recursively by the formula

`f(n) = 0.3 \cdot f(n-1)` .....[1 ] where, n is an integer and n> 0.

Substitute n = 6 in [1] we have;

`f(6) = 0.3 \cdot f(5)`

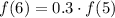
Using f(5) = 12 we have;

`f(6) = 0.3 \cdot 12`

⇒
`f(6) =3.6`

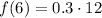
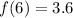
We have to find f(7).

Substitute n = 7 in [1] we have;

`f(7) = 0.3 \cdot f(6)`

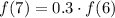
Substitute the given values f(6) = 3.6 we have;

`f(7) = 0.3 \cdot 3.6`

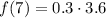
Simplify:

f(7) = 1.08

Therefore, the value of f(7)to the nearest hundredth is, 1.08