If F'(x)=\sqrt{1+x^(3) } and F(1)=5, then F(3)= (A)1.230 (B)3.585 (C)6.230 (D)8.535 (E)11.230

Question

If F'(x)=
`\sqrt{1+x^(3) }` and F(1)=5, then F(3)=

(A)1.230
(B)3.585
(C)6.230
(D)8.535
(E)11.230

Answer 1

E

Explanation:

Since the given expression is an elliptic integral, it's not easy to find F(x) explicitly. However, if we use a linear approximation, we can try to estimate F(3), though it won't be too close, since 3 is not very close to 1.

At the point (1,5) the slope of the tangent line is F'(1) =
`√(2)`

So, using that line,

F(3) = F(1) + F'(1)(3-1) = 5+2
`√(2)` = 7.828

Well, that didn't work out too well.

So, let's pull out our handy integral calculator, and we find that

`\int\limits^0_1 {√(1+x^3) } \, dx = 1.111`

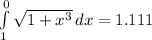
But, we know that F(1) = 5. So we need to add C = 3.889

Now, integrating again,

`\int\limits^0_3 √(1+x^3) \, dx = 7.341 + 3.889 = 11.229`

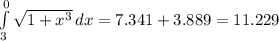
Oops. I messed up the limits, but you get the idea.