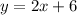Question

find the equation of the line that passes through P(7,20) and Q the midpoint of R (-3,5) and S (5,11)

Answer 1

`R (-3,5), \ \ \ S (5,11) \ midpoint \ of \ R \ and \ S \\ \\ Midpoint \ Formula \\\\(x,y)= \left ( (x_(1)+x_(2))/(2),\frac {{}y_(1)+y_(2)}{2} \right ) \\ \\Q= \left ( \frac {-3+5}{2},\frac { 5+11}{2} \right ) \\ \\Q= \left ( \frac {2}{2},\frac { 16}{2} \right ) \\ \\Q= \left ( 1 ,8) \right )`


`the \ equation \ of \ the \ line \ that \ passes \ through \ P(7,20) \ and \ Q (1,8)\\\\First \ find \ the \ slope \ of \ the \ line \ thru \ the \ points \: \\ \\ m= (y_(2)-y_(1))/(x_(2)-x_(1) ) \\ \\m=( 8-20)/(1-7 ) =(-12)/(-6)=2\\\\the \ slope \ intercept \ form \ is : \\ \\ y= mx +b \\\\20=2\cdot 7+b \\\\20=14+b\\\\b=20-14\\b=6\\\\y=2x+6`

Answer 2

First we have to find midpoint of R and S.
We can use formula such for it.
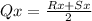
`Qx= (Rx+Sx)/(2)` and
`Qy= (Ry+Sy)/(2)`.
We obtained coordinates of point Q

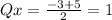
`Qx= (-3+5)/(2)=1` and
`Qy= (5+11)/(2)=8`

Now, we can find the line equation using formula y=ax+b.
We can substitute coordinates of P and Q to this formula and solving system of equation get the answer.

After substituting we obtaind such system

`\left \{ {{20=7a+b } \atop {8=a+b}} \right.`

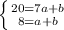
From the system of equation we obtain result

`\left \{ {{a=2} \atop {b=6}} \right.`

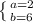
Now we can put our resuts to general line equation.

`y=2x+6`