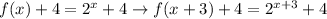Question

Explain how you would complete the translation of an exponential function using the mapping statement f(x)→f(x+k1)+k2. Does it matter which direction is translated first? Why or why not? Give examples to support your answer

Answer 1

First, in the exponent, substitute x by x+k1. Then add k2.

The order in which you apply the translations is not important. When you substitute x by x+k1, you are translating the function horizontally to the left k1 units. When you add k2, you are translating the function vertically up k2 units. Obviously, the order is nor important.

Example:

Let
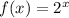
`f(x)=2^x`, k1=3, and k2=4.

Substitute x by x+3:


`f(x)=2^x \rightarrow f(x+3)=2^(x+3)`

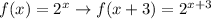
Add 4:


`f(x+3)=2^(x+3) \rightarrow f(x+3)+4=2^(x+3)+4`

In reverse order:

Add 4:


`f(x)=2^x \rightarrow f(x)+4=2^x+4`

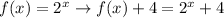
Substitute x by x+3:


`f(x)+4=2^x+4 \rightarrow f(x+3)+4=2^(x+3)+4`