Question

If f(x)=4x-6/x, what is the average rate of change of f(x) over the interval [-3,6]?

A:1/3
B:1/9
C:-1/3
D:-3

Answer 1

the correct answer is C.
Hope this helps

Answer 2

Answer: The correct option is (C)
`-(1)/(3).`

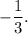
Step-by-step explanation: We are given a function f(x) defined as follows :

`f(x)=(4x-6)/(x).`

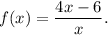
We are to find the average rate of change of f(x) over the interval [-3, 6].

We know that'

the average rate of change of a function p(x) over an interval [a, b] is given by

`A_v=(p(b)-p(a))/(b-a).`

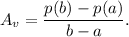
For the given function, we have

`f(-3)=(4*(-3)-6)/(-3)=(-18)/(-3)=6,\\\\\\ f(6)=(4*6-6)/(6)=(18)/(6)=3.`

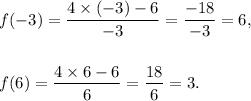
Therefore, the required average rate of change over the interval [-3, 6] will be

`A_v=(f(6)-f(-3))/(6-(-3))=(3-6)/(6+3)=-(3)/(9)=-(1)/(3).`

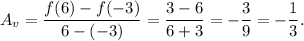
Thus, the required average rate of change over the interval [-3, 6] is
`-(1)/(3).`

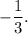
Option (C) is CORRECT.