Answer:
The standard form of the equation of a parabola is

Explanation:
Given : The vertex form of the equation of a parabola is
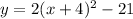 .
.
To find : What is the standard form of the equation?
Solution :
The standard form of the equation of a parabola is the expansion of the vertex form,
Now, we open the square term of the vertex form and solve it
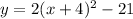
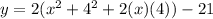
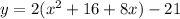
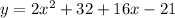

Therefore, The standard form of the equation of a parabola is
