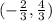Question

What are the coordinates of the centroid of a triangle with vertices J(−4, 2) , K(2, 4) , and L(0, −2) ?

Answer 1

Given the coordinates of the three vertices of a triangle ABC,
the centroid coordinates are (x1+x2+x3)/3, (y1+y2+y3)/3
so (-4+2+0)/3=-2/3, ]2+4+(-2)]/3=4/3
so the coordinates are (-2/3, 4/3)

Answer 2

ANSWER

The centroid of triangle JKL is


`(-(2)/(3),(4)/(3))`

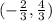
Step-by-step explanation

The centroid is the point where the medians of the triangle will intersect.

The median is the line from one vertex of the triangle and goes through the midpoint of the opposite side of the triangle.

So we find any two midpoints as follows;

Midpoint of K(2,4) and L(0,-2).


`N=((0+2)/(2),(-2+4)/(2) )=(1,1)`

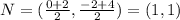
Midpoint of J(-4,2) and K(2,4),


`M=((-4+2)/(2),(2+4)/(2) )=(-1,3)`

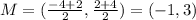
We now find the equation of the line that passes through J(-4,2) and N(1,1)

The slope is
`m=(1-2)/(1--4) =-(1)/(5)`

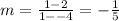
We use the point-slope form formula,


`y-y_1=m(x-x_1)`


`\Rightarrow y-1=-(1)/(5)(x-1)`


`\Rightarrow 5y-5=-(x-1)`


`\Rightarrow 5y=-x+1+5`


`5y=-x+6--(1)`

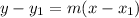
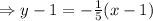
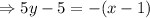
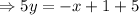
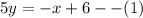
We also find the equation through L(0,-2) and M(-1,3)

The slope is
`m=(3--2)/(-1-0) =-5`

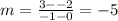
We use the point-slope form formula,


`y-y_1=m(x-x_1)`


`\Rightarrow y-3=-5(x+1)`


`\Rightarrow y-3=-5x-5`


`\Rightarrow y=-5x-5+3`


`\Rightarrow y=-5x-2--(2)`

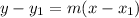
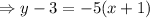
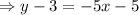
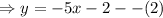
We substitute equation (2) in equation (1),

This gives us,


`\Rightarrow 5(-5x-2)=-x+6`


`\Rightarrow -25x-10=-x+6`


`\Rightarrow -25x+x=6+10`


`\Rightarrow -24x=16`

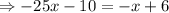
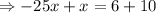
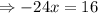
We divide both sides by -24 to obtain,


`x=-(2)/(3)`

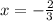
We substitute
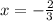
`x=-(2)/(3)` in to equation (2) to obtain,


`\Rightarrow y=-5(-(2)/(3))-2`


`\Rightarrow y=(10)/(3)-2`


`\Rightarrow y=(4)/(3)`

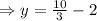
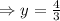
Therefore the centroid is


`(-(2)/(3),(4)/(3))`