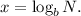Question

Express this equation in logarithmic form. b^x = N

Answer 1

`b {}^(x) = n \\ taking \: log \: on \: both \: the \: sides \: \\ log(b {}^(x) ) = log(n) \\ x( log(b) ) = log(n) \\ x = ( log(n) )/( log(b) ) \\ x = log_(b)(n)`

Answer 2

Answer: The required logarithmic form of the given equation is
`x=\log_bN.`

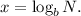
Step-by-step explanation: We are given to express the following equation in logarithmic form :

`b^x=N~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

We know that

The logarithmic form of an exponential equation
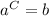`a^C=b` is given by

`C=\log_ab.`

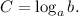
So, from equation (i), we get

`b^x=N\\\\\Rightarrow x=\log_bN.`

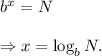
Thus, the required logarithmic form of the given equation is
`x=\log_bN.`