to the risk of sounding redundant.
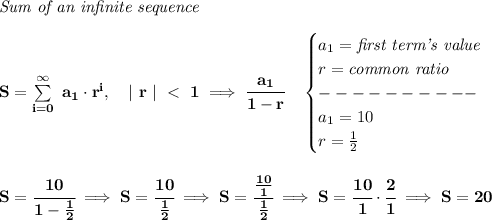
notice it goes from 10, to 5, to 2.5 and so forth, the next term is half the previous one, namely the multiplier, or "common ratio" is 1/2.
10 * 1/2 is 5, 5 * 1/2 is 2.5 and so on.
now, the Sum is going to infinity, however, when the common ratio is a fraction less than 1 and more than 0, either negative or positive, it is
convergent, namely it reaches a limit, it doesn't go to neverland.
so, in this case, the common ratio is indeed | r | < 1, and therefore, it does reach a limit, keeping in mind the first term's value is 10.