Question

Verify the identity. cos(x)/(1+sin(x))+(1+sin(x))/cos(x)=2sec(x)

Answer 1

The identity we want to verify is:


`\displaystyle{ (\cos x)/(1+\sin x) + (1+\sin x)/(\cos x) =2\sec x`.

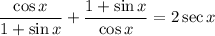
Note that sec(x)=1/cosx, so we write the right hand side as 2/(cos(x)).


We multiply the first expression by (cosx)/(cosx), and the remaining two by (1+sinx)/(1+sinx) to have them in common numerators:


`\displaystyle{ (\cos^2x)/((\cos x)(1+\sin x)) + ((1+\sin x)^2)/((\cos x)(1+\sin x)) = (2(1+\sin x))/((\cos x)(1+\sin x))`.

Now we can only consider the numerators. The right hand side, expanding (1+sinx)^2 becomes:


`\cos^2x+1+2\sin x+\sin^2x`.

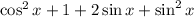
From the identity
`\sin ^2x+\cos^2x=1`, the expression further simplifies to:


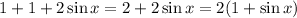
`1+1+2\sin x=2+2\sin x=2(1+\sin x)`. This proves the identity.