Question

If y varies directly with x and y=10 when x=5, what is the value of k?

Answer 1

`\bf \qquad \qquad \textit{direct proportional variation}\\\\ \textit{\underline{y} varies directly with \underline{x}}\qquad \qquad y=kx\impliedby \begin{array}{llll} k=constant\ of\\ \qquad variation \end{array}\\\\ -------------------------------\\\\ \textit{we know that } \begin{cases} y=10\\ x=5 \end{cases}\quad 10=k5\implies \cfrac{10}{5}=k\implies 2=k`

Answer 2

Answer: The required value of k is 2.

Step-by-step explanation: Given that y varies directly as x and y = 10 when x = 5.

We are to find the value of k, the constant of variation.

According to the given information, we have

`y\propto x\\\\ \Righatrrow y=k* x\\\\ \Rightarrow y=kx`

y = 10 when x = 5, so we get from above equation

`10=k* 5\\\\\Rightarrow k=(10)/(5)\\\\\Rightarrow k=2.`

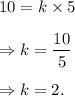
Thus, the required value of k is 2.