Question

A fourth degree polynomial with five terms could have, at most, how many different linear factors? 2 3 4 5

Answer 1

The answer would be 4

Answer 2

4

Explanation:

We are given a polynomial of degree 4 with five terms.

We have to find atmost number of different linear factors.

Let the polynomial of degree 4 with 5 terms

`x^4+bx^3+cx^2+dx+e`

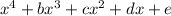
It can be written as the product of linear factors

`(px-u)(qx-v)(rx-w)(sx-y)`

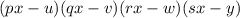
We know that

Number of linear factors=Degree of polynomial

Consider , a quadratic polynomial

`x^2+3x+2`

`(x+2)(x+1)`

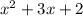
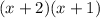
Degree of polynomial=2

Number of linear factors=2

Degree of polynomial=Number of linear factors

Hence, the polynomial could have atmost different linear factors=4