Question

Factor completely, then place the answer in the proper location on the grid.

9x^4 - 225y^8

please help!

Answer 1

`\mathrm{Factor\:out\:common\:term\:}9 \ \textgreater \ 9\left(x^4-25y^8\right)`


`Factor \ \textgreater \ x^4-25y^8`


`\mathrm{Apply\:difference\:of\:squares\:rule:\:}x^2-y^2=\left(x+y\right)\left(x-y\right)`

`x^2-5y^4=\left(x+√(5)y^2\right)\left(x-√(5)y^2\right)`


`x^2-5y^4 \ \textgreater \ \mathrm{Apply\:difference\:of\:squares\:rule:\:}x^2-y^2=\left(x+y\right)\left(x-y\right)`

`x^2-5y^4=\left(x+√(5)y^2\right)\left(x-√(5)y^2\right)`


`\left(x^2+5y^4\right)\left(x+√(5)y^2\right)\left(x-√(5)y^2\right)`


`9\left(x^2+5y^4\right)\left(x+√(5)y^2\right)\left(x-√(5)y^2\right)`

Hope this helps!

Answer 2

The expression 9x^4 - 225y^8 can be factored as
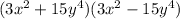`\((3x^2 + 15y^4)(3x^2 - 15y^4)\)` using the difference of squares formula. This represents the product of two binomials, each corresponding to the sum and difference of square terms.

To factor the expression
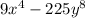`9x^4 - 225y^8`, we can use the difference of squares formula:

`a^2 - b^2 = (a + b)(a - b)`

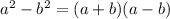
In this case,
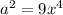`\(a^2 = 9x^4\)` and
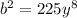`\(b^2 = 225y^8\)`. We can rewrite the expression as:

`\[ 9x^4 - 225y^8 = (3x^2)^2 - (15y^4)^2 \]`

Now, we can apply the difference of squares formula:

`\[ 9x^4 - 225y^8 = (3x^2 + 15y^4)(3x^2 - 15y^4) \]`

So, the factored form is
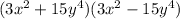`\((3x^2 + 15y^4)(3x^2 - 15y^4)\)`.