Question

Use a table to solve. round to the nearest tenth 2^(8x)=93

Answer 1

I got the decimal form where x= 0.817395
if that's wrong then sorry

Answer 2

`x\approx 0.8`

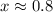
Explanation:

The given expression is

`2^(8x)=93`

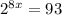
To solve this we have to apply logarithms as follows

`2^(8x)=93\\ln(2^(8x))=ln(93)`

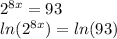
Now, applying properties of logarithms, we have

`ln(2^(8x))=ln(93)\\8x(ln2)=ln(93)\\x=(ln93)/(8(ln2))\\ x\approx 0.8`

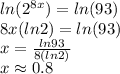
Therefore, the answer rounded to the nearest tenth is

`x\approx 0.8`

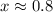
Remember that you have to apply logarithms when the exponential equation cannot be expressed as equivalent powers.