Question

Why is the product of two rational numbers always rational? Select from the Bold words to correctly complete the proof.

Let ab and cd represent two rational numbers. This means a, b, c, and d are (Integers or irrational numbers), and (b is not 0, d is not 0 or b and d are 0). The product of the numbers is acbd, where bd is not 0. Because integers are closed under (addition or multiplication), ​acbd ​ is the ratio of two integers, making it a rational number.

Answer 1

Integers, d is not zero, multiplication.

Answer 2

Product of two rational numbers always Rational:

As given
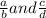`(a)/(b) and (c)/(d)` are two rational numbers.

So, all a,b,c,d are integers such that b ≠ 0, and d≠ 0.

So the product of
`(a)/(b)*(c)/(d)=(ac)/(bd)` such that bd≠ 0.→→[Integers are closed under multilication i.e follows commutative property under multiplication]

→ Which shows that
`(ac)/(bd)` is rational number.