Question

Use synthetic division to determine whether the number k is an upper or lower bound (as specified for the real zeros of the function f). k = 2; f(x) = 5x4 + 4x3 - 2x2 + 2x + 4; Upper bound?

Answer 1

No, it is a lower bound.

Answer 2

The given Polynomial is :

`f(x) = 5x^4 + 4x^3 - 2x^2 + 2x + 4=5( x^4 + (4)/(5)x^3 - (2)/(5)x^2 + (2)/(5)x + (4)/(5))`

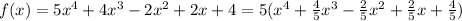
By Rational Root theorem the of Zeroes of the Polynopmial are:

`\pm(1)/(5),\pm(2)/(5),\pm(4)/(5),\pm1,\pm2,\pm4`

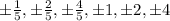
But ,
`f(\pm(1)/(5),\pm(2)/(5),\pm(4)/(5),\pm1,\pm2,\pm4)\\eq 0`

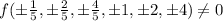
So, no root of this polynomial is real.

Therefore, All the four roots of Polynomial are imaginary.

So, we can't say whether the number k=2, is an upper or lower bound of the polynomial
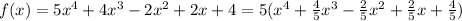`f(x) = 5x^4 + 4x^3 - 2x^2 + 2x + 4=5( x^4 + (4)/(5)x^3 - (2)/(5)x^2 + (2)/(5)x + (4)/(5))`.