Answer:
option (b) is correct.
The product of
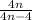 and
and
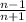 is
is

Explanation:
Given
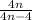 and
and
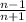
We have to find the product of given two terms that is

Consider the product written as ,

Taking 4 common from the denominator of first term and simplify the first expression , we have,
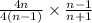
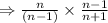
(n-1 ) in numerator get canceled by (n-1 ) in denominator, we have,
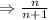
Thus, option (b) is correct.
The product of
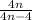 and
and
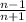 is
is
