Question

The focus of a parabola is (-10, -7), and its directrix is x = 16. Fill in the missing terms and signs in the parabola's equation in standard form. (y )^2= (x )

Answer 1

First, we determine if the parabola is "horizontal" or "vertical", as the directrix is a vertical line, this implies the parabola is "horizontal".

We know that the focus is at the left of the parabola, this tells us that the parabola opens to the left.

We find the distance from the focus to the directrix:


`\sqrt{ (-10-16)^(2) } =26`

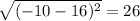
Half of this distance must be the distance from the focus to the vertex, so the vertex of the parabola is the point (3,-7).

This means the vertex form of the equation for the parabola is:


`x=-a(y+7)^2+3`


`a` is an arbitrary positive value that determines how "curved" the parabola is, we can only find this value if we know a point of the parabola.

We write the vertex equation in standard form:


`x=-ay^2-14ya-49a+3`

Attached is a plot of the parabola if
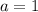
`a=1`. It has the directrix, focus, and vertex labeled.

Answer 2

Answer: (y+7)^2= -52(x-3)

Explanation: