Answer:
The students scoring more than 366 will be best 80%of all applicants.
Explanation:
We are given the following information in the question:
Mean, μ = 426
Standard Deviation, σ = 72
We are given that the distribution of score is a bell shaped distribution that is a normal distribution.
Formula:
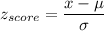
We have to find the value of x such that the probability is 0.2
P(X < x)
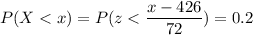
Calculation the value from standard normal z table, we have,
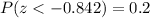
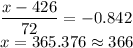
Hence, the the passing score is 366 or higher. The students scoring more than 366 will be best 80%of all applicants.