Question

The system of equations shown is solved using the linear combinations method

Answer 1

There are an infinite amount of solutions to the system because the equations represent parallel lines. Whenever you get a true statement like 0 = 0, you know that there are infinitely many solutions. This is because the equations represent lines that never intersect, which are parallel lines. Remember that ALL lines go on forever, they never end.

Answer 2

There are infinitely solutions to the system because the equations represent the same line.

Explanation:

The system of linear equations presented represents the same line. We can deduct that by multiplying the first one by -4:

`(6x-5y=-8)(-4)\\-24x+20y=32`

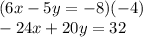
As you can observe, we get the same equation than the second one in the system, this means that they actually represent the same line. In other words, the solutions are all the common points, which are all of them possible, which are infinite.

Therefore, the right option is the last one.