Question

Eight people audition for a choir. The choir director must choose one soprano, one altar and one soprano. In how many ways can the director fill these positions?

Answer 1

There are 72 different ways the director can fill the positions.

(1+2+3+4+5+6+7+8) x 2


You multiply it by 2 because there are going to be 4 other people who will not have a position, and 8/4 is 2.

Answer 2

Since the the people are not auditioning for the same position, the order in which they are selected matters. This tells us that we have to calculate the permutation of 8 objects taking 3 at a time. The permutation of n objects taking r at a time is given by the formula
`P(n,r)=(n!)/((n-r)!) \\P(8,3)=(8!)/((8-3)!) =(8*7*6*5!)/(5!) =8*7*6=336`

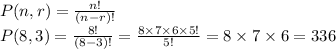
The director can fill these positions in 366 ways.

A quicker way to solve this problem would have been to realize that there are 8 ways to fill the first position. Once the first position has been filled, there are 7 ways to fill the second position. Once the second position has been filled, there 6 ways to fill the third position. The total number of ways to fill the positions will then be
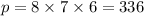`p=8*7*6=336`. Both ways of working this problem out are valid.