Answer:
The reason for ∠5≅∠3 is Alternate Interior Angles Theorem and the reason for ∠8+120°=180° is Substitution Property of Equality.
Explanation:
It is given that the lines m and n are parallel to each other. The measure of angle 3 is 120 degree.
From the figure it noticed that the p is a transversal line intersecting the lines m and n.
According to the Alternate Interior Angles Theorem, if a transversal line intersect two parallel lines then the alternate interior angles are same.
By Alternate Interior Angles Theorem


Therefore, the reason for ∠5≅∠3 is Alternate Interior Angles Theorem.
Since the measure of angle 3 is 120 degree.
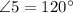
The angle 5 and 8 lies on a straight line, so by Linear Pair Postulate,
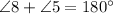
Use Substitution Property of Equality and substitute
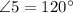 .
.
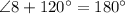
Using Subtraction Property of Equality

Therefore the reason for ∠8+120°=180° is Substitution Property of Equality.