Question

The length of a rectangular field is represented by the expression14x-3x^2+2y. The width of the field is represented by the expression 5x-7x^2+7y. How much greater is the length of the field than the width?

A) 9x+4x^2-5y
B)9x-10x^2-5y
C)19x+4x^2+9y
D) 19x-10x^2+9y

Answer 1

The length of the rectangular field is
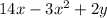
`14x-3x^2+2y`, and the width is
`5x-7x^2+7y`.

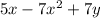
To find how much greater is the length of the field than the width we need to subtract the width from the length, so we have:


`(14x-3x^2+2y)-(5x-7x^2+7y)=(14x-3x^2+2y)-5x+7x^2-7y`.

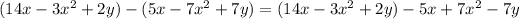Operating with the equal degree and variable terms, this difference is equal to


`(14x-5x)+(7x^2-3x^2)+(2y-7y)=9x+4x^2-5y`


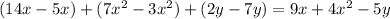
Answer: A