Question

Given: /|| m

Assume the transversal is perpendicular to m. Find m1.
A. 30
B. 45
C. 60

Answer 1

Answer: The correct option is (C) 60°.

Step-by-step explanation: Given that the line l is parallel to the line m and the transversal is perpendicular to m.

We are to find the measure of angle 1.

Since the transversal is perpendicular to line m, so it must be perpendicular to line l because lines l and m are parallel.

Also, we have one more transversal, which is inclined at an angle of 30° to line m, so it must inclined at an angle of 30° to line l also, since both the angles will be corresponding.

Therefore, we have

`m\angle 1+30^\circ=90^\circ\\\\\Rightarrow m\angle 1=90^\circ-30^\circ\\\\\Rightarrow m\angle 1=60^\circ.`

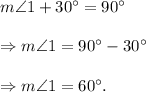
Thus, the measure of angle 1 is 60°.

Option (C) is CORRECT.

Answer 2

ANSWER

`m \: < \: 1 = 60`

Step-by-step explanation

Since the transversal is perpendicular to m,
it implies that the triangle formed by the perpendicular transversal, the slant transversal and the line m is a right angle triangle.



We use vertically opposite angles property to bring m<1 in to the right triangle.


We now use the sum of interior angles property to obtain,


`m \: < \: 1 + 30 + 90 = 180`

This implies that,



`m \: < \: 1 + 120 = 180`


We group like terms to obtain,


`m \: < \: 1 = 180 - 120`


This means that,


`m \: < \: 1 = 60`


We could have also used corresponding angles property, then


`m \: < \: 1 + 30 = 90`



`m \: < \: 1 = 90 - 30`




`m \: < \: 1 = 60`