Question

Divide the following polynomial using synthetic division, then place the answer in the proper location on the grid. Write answer in descending powers of x. (x3 + 6x2 + 3x + 1 ) ÷ (x - 2)

Answer 1

x^2+8x+19+39/(x-2)
I cant show how to use synthetic unless I attach a file

Answer 2

[1.(x)²+ 8.(x) + 19] +
`(39)/((x - 2))`

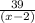
Explanation:

The given polynomial is (x³+ 6x²+ 3x + 1) and we have to divide this polynomial by (x - 2) using synthetic division.

In synthetic division, we divide coefficients of the given terms of the polynomial by (x -2) = 0 ⇒ x = 2

So, 2| 1 6 3 1 ---------[ coefficients]

2 16 38

1 8 19 39

Let me explain it. In first row i have written the coefficients of the terms given in the polynomial 1.x³ + 6.x² + 3x + 1

In the first row I have written 2 in the left side before 1. This is the number by which i am going to divide the coefficients written in the first row.

Now I copied 1 at the bottom (below the line).

Then 2×1 = 2 (written in second row) added with 6 gave 8 at the bottom.

then 8×2 = 16 (written in second row) added with 3 gave 19 at the bottom.

19×2 = 38 (written in second row) added with 1 gave 39 at the bottom.

Now we will rewrite the expression

[1.(x)²+ 8.(x) + 19] +
`(39)/((x - 2))`

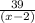
Here highlighted part give in the bracket is the quotient and 19 is the remainder.