Question

N=3, zeros 4 and 2i, f(2)=-48 find nth degree polinomonal function

Answer 1

The degree is 3, the zeros are; 4, 2i, -2i and a point is (-48, 2)

For zeros; 2i, -2i <-- complex conjugates, always in pairs


`(c)/(a)=(2i)(-2i)`
= -4(i²=-1)
=5


`(b)/(a)=-(2i+(-2i))`
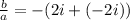
=0

Therefore the equation is; a(
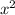
`x^(2)`+5) <-- b value is zero

Rewrite the equation with all zeros;

a(x-4)(x²+5)=f(x) <-- put in coordinates of the points to find the value of x
a(2-4)(2²+5)=-48
a(2)(9)=-48
a=-48/18
a=-8/3

The final polynomial function is; (-8/3)(x-4)(x²+5)=f(x)

Hope I helped :)