Question

A quadratic equation of the form 0 = ax2 + bx + c has a discriminant value of 0. How many real number solutions does the equation have?

Answer 1

it has one solution. when discriminant=0, tangent to the curve( means touches at one point ) hence one solution.

Answer 2

we know that

the formula to solve a quadratic equation of the form
`ax^(2)+bx+c=0` is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}}{2a}`

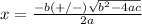
The discriminant is equal to

`(b^(2)-4ac)`

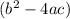
If the discriminant is equal to zero

then

`(b^(2)-4ac)=0`

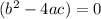
substitute in the formula

`x=(-b(+/-)√(0))/(2a)`

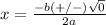
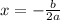`x=-(b)/(2a)`-------> only one real number solution

therefore

the answer is

the number of solutions is equal to
`1`