Question

A study of six hundred adults found that the number of hours they spend on social networking sites each week is normally distributed with a mean of 17 hours. the population standard deviation is 6 hours. what is the margin of error for a 95% confidence interval? 0.134 0.220 0.313 0.480

Answer 1

The answer is C. 0.313

Answer 2

0.48

Explanation:

Given : Mean = 17 hours

Standard deviation = 6 hours

n = population size =600

To Find: what is the margin of error for a 95% confidence interval?

Solution:

n= 600

`\sigma = 6`

z = 1.96 for a 95 % confidence interval;

Margin of error formula:

`ME=(z * \sigma)/(√(n))`

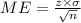
Substitute the values

`ME=(1.96 * 6)/(√(600))`

`ME=0.48`

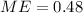
Hence the margin of error for a 95% confidence interval is 0.48