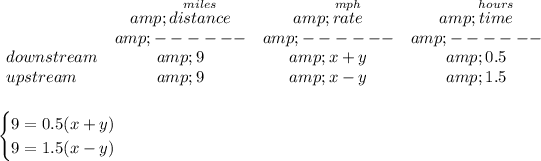Question

motorboat travels 9 miles downstream (with the current) in 30 minutes. The return trip upstream (against the current) takes 90 minutes. Which system of equations can be used to find x, the speed of the boat in miles per hour, and y, the speed of the current in miles per hour? Recall the formula d = rt. 9 = 0.5(x – y) 9 = 1.5(x + y) 9 = 1.5(x – y) 9 = 0.5(x + y) 0.5 = 9(x – y) 1.5 = 9(x + y) 1.5 = 9(x – y) 0.5 = 9(x + y)

Answer 1

do recall d = rt.

keeping in mind that the boat though it has a speed of "x", when is going with the current is really going faster, if the current has a speed of "y", then the boat is really going downstream at "x + y".

going upstream, is going against the current, and thus its speed is "x - y" then.

now, notice, the time will be in hours, since the rate is also in hours, mph, thus 30 minutes is 0.5 or half an hour, whilst 90 minutes is 1.5 or one hour and a half.


`\bf \begin{array}{lccclll} &\stackrel{miles}{distance}&\stackrel{mph}{rate}&\stackrel{hours}{time}\\ &------&------&------\\ downstream&9&x+y&0.5\\ upstream&9&x-y&1.5 \end{array} \\\\\\ \begin{cases} 9=0.5(x+y)\\ 9=1.5(x-y) \end{cases}`