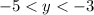Answer:
1. 13 or -13
2. -5 < y < -3
3. 6 or -6
4. 1/8 or -1/8
Explanation:
Clear the absolute-value bars by splitting the equation into its two cases, one for the Positive case and the other for the Negative case.
The Absolute Value term is |x|
For the Negative case we'll use -(x)
For the Positive case we'll use (x)
Step 3 :
Solve the Negative Case
-(x) = 13
Multiply
-x = 13
Multiply both sides by (-1)
x = -13
Which is the solution for the Negative Case
Step 4 :
Solve the Positive Case
(x) = 13
Which is the solution for the Positive Case
Step 5 :
Wrap up the solution
x=-13
x=13
But for the case of question (2) its a different pattern..
Since this is a "less than" absolute-value inequality, my first step is to clear the absolute value according to the "less than" pattern. Then I'll solve the linear inequality.
| y + 4 | < 1
–1 < y + 4 < 1
This is the pattern for "less than". Continuing, I'll subtract 3 from all three "sides" of the inequality:
–1 – 4 < y + 4 - 4 < 1 – 4
–5 < y < -3
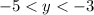
The solution to the original absolute-value inequality, | y + 4 | < 1 , is the interval: