Question

What is the sum of the infinite geometric series? -3-3/2-3/4-3/8-3/16

Answer 1

hmmm
`\bf -3~,~-\cfrac{3}{2}~,~-\cfrac{3}{4}~,~-\cfrac{3}{8}~,~-\cfrac{3}{16}`

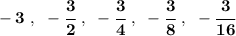
now, if you notice the terms there.... since we know is a geometric sequence/serie, we can tell there's a "common multiplier" namely a "common ratio", and if you divide any two terms, the latter by the former, the quotient you get is, yes, you guessed it, is the "common ratio", let's check about.


`\bf -\cfrac{3}{2}/ -3\implies \cfrac{1}{2}\qquad \qquad -\cfrac{3}{4}/ -\cfrac{3}{2}\implies \cfrac{1}{2}`

so, as you can see, the "common ratio" is then, just 1/2.

now, for a geometric serie, whose common ratio is a fraction, namely less than 1 and greater than 0, then


`\bf \textit{sum of an infinite geometric serie}\\\\ S=\sum\limits_(i=0)^(\infty)~a_1\cdot r^i\implies \cfrac{a_1}{1-r}\quad \begin{cases} a_1=\textit{first term's value}\\ r=\textit{common ratio}\\ \qquad 0\ \textless \ |r|\ \textless \ 1\\ ----------\\ a_1=-3\\ r=(1)/(2) \end{cases} \\\\\\ S=\cfrac{-3}{1-(1)/(2)}\implies S=\cfrac{-3}{(1)/(2)}\implies S=-6`

Answer 2

Answer: -6.

Step-by-step explanation: Given geometric series is-

`-3,~-(3)/(2), ~-(3)/(4), ~-(3)/(8),~-(3)/(16),...`

Here, the first term of the series,
`a=-3`

and the common ratio,
`r=(1)/(2).`

Since it is an infinite series, so sum is given by

`S=(a)/(1-r)\\\\\\\Rightarrow S=(-3)/(1-(1)/(2))\\\\\\\Rightarrow S=(-6)/(2-1)\\\\\\\Rightarrow S=-6.`

Thus, the sum of the series is -6.