Question

For the given function, find the vertical and horizontal asymptote(s) (if there are any). f(x) = the quantity x squared plus three divided by the quantity x squared minus nine

Answer 1

The vertical asymptotes are: "x = 3" and "x = -3" .
__________________________________________
The horizontal asymptote is: "y = 2" .
___________________________________________
Step-by-step explanation:
___________________________________________

f(x) =
`(x^(2)+ 3)/( x^(2) - 9)` ;

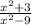
We know that "(x² − 9) ≠ 0 ; since we cannot divide by "0" ; so the "denominator" in the fraction cannot be "0" ;

since: 9 − 9 = 0 ; "x² " cannot equal 9.

So, what values for "x" exist when "x = 9" ?

x² = 9 ;

Take the square root of EACH SIDE of the equation ; to isolate "x" on one side of the equation ; and to solve for "x" ;

√(x²) = √9 ;

x = ± 3
__________________________________________
So; the vertical asymptotes are: "x = 3" and "x = -3" .
__________________________________________
The horizontal asymptote is: "y = 2" .
__________________________________________
(since: We have: f(x) =
`(x^(2)+ 3)/( x^(2) - 9)` ;

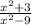The "x² / x² " as the highest degree polymonials; both with "implied" coefficients of "1" ; and both raised to the same exponential power of "2".